I posted a while back about how through perseverance it's possible to work in a medium like MS Paint. I thought I might show a similar process this time but with the benefit of working with a tablet in photoshop.
If you click on the first picture you should be able to scroll through them and see the painting come together. On average, there's about 30 minutes of work between each shot.
Hopefully this perspective reveals something of how the magic trick works.
I often take a lot of shortcuts with digital, but this time I decided to just use the source photo for visual reference, rather than incorporating it in any way back into the painting.
Cheers!
The concise, illustrative and phenomenally interesting discussion of foibles in fine art
Monday, 24 November 2014
Sunday, 23 November 2014
Mathematical!
At the beginning of this year I was sitting at work, waiting
for the hours to tick by, when I began to wonder what I would do if I
discovered I was immortal. Many scientists have believed for some time that the
first person to live to be 200 has already been born, so it may not even be as
impossible a situation as it sounds. I figured the key thing for an immortal
would be capitalising on long-term investment. Money is certainly a nice thing
to have a lot of, but surely the novelty would soon wear off and the eons of
malaise would set in.
I would need a good hobby to stay occupied throughout the
millennia, so I figured I would learn everything. Take every course under the
sun and become a specialist in every field. The more I thought about it, the
more it made sense, and then another though occurred. What if I set out on this
quest for ultimate smarts and then, only later, discovered I was not immortal?
Then I would have spent a lifetime of optimistic work, chasing a dream. Life is
probably longer than it seems, so why not live like it’s endless?
I decided to go back to uni and study something new. As I
have a degree in visual-arts, I thought I’d go the other way and begin again in
science.
Maths was an interesting option. I’d liked maths as a kid,
but by high school it had started to seem like an endless chore. Maybe there
was more to it. And as an immortal I could afford to give it another look.
Unfortunately maths at ANU is not exactly child’s-play.
Taking an English class is not easy, but if you don’t speak the language it’s
practically impossible. Having not studied tertiary maths I did not speak the
language, and the serious courses required a double-major in college maths.
Also, I happened to be considering all of this just two weeks before the beginning
of classes.
I submitted a very late application for a bachelor of
science at ANU and turned to the internet to see if it was possible to learn
maths in a fortnight.
Fortunately, Khan Academy.
That guy will learn you brains you didn’t know what were.
I spent about 10-12 hours a day working through the courses.
My application for uni was successful and I signed up for maths. The first
thing the course provided was a general test designed to outline what you
should know. I passed, and the course began. I also took psychology, biology
and physics. The first two were simple enough because they didn’t require a lot
of pre-knowledge, but physics needed both maths and physics experience. The
courses started at the beginning anyway, but maths and physics took off at a
blistering pace. I had to work harder than I’ve ever worked on anything, but I
kept up. I never really got ahead of the curve in physics but maths started to
fall into place, and I wound up getting a HD.
For the first time I saw math teachers who actually cared
about maths, and I started to get a glimpse of the depth of the subject. The
biggest change, though, came from reading Paul Lockhart’s book, which shows the
fundamentally aesthetic nature of maths, and how poorly this tends to be communicated
in school.
I’m definitely hooked on this approach now, and I thought
I’d attempt to explain through a problem that I came up with myself.
Introducing; Simon’s Marvellous Math Problem of Fantastical
Wonder.
The problem follows as such:
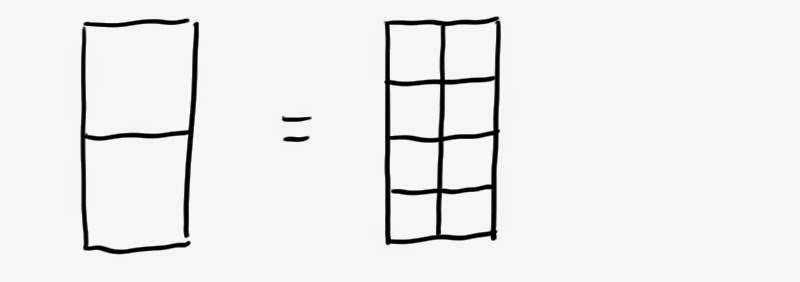
If you take two standard A4 sheets of paper, and put them next to each other with the short sides at the top, this makes an A3 sheet of paper. The interesting thing about this is, the A3 sheet is the same shape as the A4, just a scaled up version. So the question is: What’s the deal with that?
If you take two standard A4 sheets of paper, and put them next to each other with the short sides at the top, this makes an A3 sheet of paper. The interesting thing about this is, the A3 sheet is the same shape as the A4, just a scaled up version. So the question is: What’s the deal with that?
The first thing to notice is that there can only be one
particular rectangle that has this property. Two squares next to each other
make a rectangle, and vice versa. So at some specific point in between a 1x1
square and a 1x2 rectangle there is a magic shape that is half of itself.
The easiest way to describe a rectangle is by the two
lengths of the sides, but in our case, it doesn’t matter what the size of the
rectangle is, only the shape. So the thing we’re looking for, the thing that
doesn’t change with the scale of the shape, is the ratio of the sides.
A 1x2 rectangle is the same shape as a 2x4 rectangle because
½ = 2/4 = 0.5
So how do we find the ratio of the sides of an A4 sheet?
We could try looking up the measurements.
International A4 size is 210 x 297mm. So the ratio of the
short side to the long side is 210/297 or
0.70707070707(repeating).
That’s cool, but what about an A3 sheet. It should be the
same ratio, right?
International A3 size is 297 x 420mm. So the ratio is 297/420
or 0.70714285714...
What we’ve discovered is that the shape of A4 paper is very
close to having the property we described, but not perfect, because
0.70707070707 is not exactly the same as 0.70714285714. So is it possible to
have a perfect ratio, and what is it, and why?!?
The first clue to working it out is that both the A4 and A3
sheets share a measurement: 297mm. This is because the long side of the A4
becomes the short side of the A3.
Knowing this we can do something tricky. If we arbitrarily
decide that the short side of the A4 is 1 unit in length (it doesn’t matter
what the unit is; 1cm or 1billion cm), then the long side is the unknown
length, which we’ll call Z. And by studying the picture below we can see
something interesting:
If the A4 shape is 1/Z, then the A3 shape can also be
described using those units. It’s short
side is Z, and it’s long side is the same as 2 A4 short sides, which makes it’s
ratio Z/2.
For the shapes to be the same, the ratios of the lengths
must be identical, which means:
The question has become; “what number must Z be to make this
statement true?”
To find this, we can alter the way we express this
statement, and “solve for Z”
Because the A3 side is “Z divided by two”, if we double
everything this comes out as
Did we get anywhere? Now Z equals two divided by Z. To get
rid of the fraction we can do the same thing again, except this time we
multiply everything by Z.
Now there’s only one Z in the equation but it’s
squared. That’s not a problem though, if
2 equals Z x Z, then that just means Z is a number that if you multiply it by
itself you get 2. Which we can express as
Now we have it. It turns out that the only ratio of lengths that
our perfect A4 rectangle can have is
So what is the square root of two?
1 * 1 = 1
1.5 * 1.5 = 2.25
So it must be between those two numbers. If we type it into
a calculator it comes out as 1.41421356237. Fair enough. Is that the end of the
story?
But what if we calculate 1.41421356237 * 1.41421356237?
This comes out as 1.99999999999.
So this can’t really be the square root of 2. The calculator
must have not given us the precise value because it can only display a limited
amount of numerals after the decimal point. So how many numerals would be
required for the precise value that is equal to the square root of two?
The answer is infinite.
Just like the value pi, which is the ratio of a circle’s circumference to it's diameter, the value equal to the square root of two cannot
be described with numerals. This type of number is called “irrational”.
Pythagoras and the some other ancient Greek lads discovered
this and came up with a proof by showing that the number could not be even, but
also could not be odd. Pythagoras actually tried to hide this fact because his
troop had developed a kind of number-based religion that stated that all values
could be expressed as fractions.
Much later down the track, a mathematician discovered that
there are actually more irrational numbers than rational ones. In fact there
are so many more irrational numbers that if you threw a dart at a number-line,
and with infinite care, found the exact value that the dart hit, the chance of
this value being a rational number (1 or 2 or ½ or 118739182/19723649872634
etc.)
Is actually zero!
So we have answered the question of what the perfect A4
shape is, but we haven’t really worked out why this is.
There is, of course, no complete answer to this question,
but still, we might be able to find some interesting clues.
One interesting thing to note is that if you have a square
with sides of length 1, the length of the diagonal is also the square root of
two (which is essentially where we get the term “square root”)
This doesn’t seem like an accident. There must be some
intrinsic connection between the two questions “How long is the diagonal in a
square?” and “How long is longer side of a shape that is equal to half of
itself?”
Now, we are in the domain of mathematics. This is what maths
is about. Maths doesn’t care what the ratio of two lengths are, it cares about
why that ratio is the way it is.
In school we’re taught algebra and the like as though
calculation is the purpose of maths. This couldn’t be more wrong. Discovering
the intrinsic nature of the realms of our thoughts is what maths is about.
But the thing is, knowing a bit of algebra enabled us to go
from a question about the shape of an A4 page to a deeper question about the
connection between two shapes and an irrational number. Without algebra and
other concepts, that journey, and the journey on from there into more
interesting questions, would be essentially impossible.
The tools of maths need to be learnt in order to ask the
interesting questions, but too many maths teachers have forgotten or have never
learnt that the tools are the means to studying maths, not the subject itself.
As to the question of the connection between our shape and
the diagonal of a square, if you have read this far you’ve proven yourself able
to take up this question yourself. But I’ll share two things that I discovered
from various ponderisations.
First, if you take a square with sides of root 2, the
diagonal is of length 2.
Tuesday, 4 November 2014
Subscribe to:
Posts (Atom)